编者注:本译文的首个版本见于此处,本次再版已经过校对。在此对原译者 kim 表示感谢。
原文的写作时间不确定,但可将其视为一个原点,反思以太坊的设计理念以及以太坊在这几年间的演化。既是反思其创新,也是反思其有欠考虑的地方。
尽管以太坊的许多理念在早先的密码学货币(如比特币)上已经运用并测试了5年之久,但从某些协议功能的处理方法上来说,以太坊与常见方式仍有许多不同。而且,以太坊可用于开发全新的经济工具,因为它具有其他系统不具备的许多功能。本文会详细描述以太坊所有的潜在优点,以及在构建以太坊协议过程中某些有争议的地方。另外,也会指出我们的方案及替代方案的潜在风险。
原则
以太坊协议的设计遵循以下几点原则:
三明治复杂模型(亦可译为 “复杂度分层模型” ):我们认为以太坊的底层协议应尽可能的简单,接口设计应易于理解(不论是面向开发者的高级编程语言接口,还是面向用户的使用接口)。那些不可避免的复杂部分应放入中间层。中间层不作文核心共识的一部分,且对最终用户不可见,它包含:高级语言编译器、参数序列化和反序列化脚本、存储数据结构模型、leveldb 存储接口以及联网协议等。当然,区分的界线不是绝对明确的,有时候需要酌情调整。
自由:不应限制用户使用以太坊协议,也不应试图优先支持或不支持某些以太坊合约或交易。这一点与 “网络中立” 概念背后的指导原则相似。比特币交易协议就 没有 遵循这一原则:比特币交易协议并不鼓励区块链的 “非常规用途(off-labal purpose)” (如,数据存储,元协议)(校对注:off-labal 的原意为将药物用在其经过批准的适应症之外的症状上,例如使用止咳药来治疗头痛。此处意译为 “非常规用途” );而且,有时候还有人用 准-协议层 的变更(例如将 OP_RETURN 字段的长度限制在 40 字节)来攻击以 “未经授权” 的方式使用区块链的应用(校对注:此处是在讽刺比特币的社区有审查比特币区块链用法的倾向)。因此,在以太坊,我们坚定支持仅使用交易手续费来达成大体激励相容的办法 —— 用户消耗整个网络越多资源,需要付出的代价就越高,也即使其自己承担成本(即庇古税)。
泛化:以太坊协议的特性和操作码应最大限度地体现低层次的概念(就像基本粒子一样),以便它们可以随意组合,包括组合出今天看来没什么用、但未来可能有用的东西。而且,通过剥离那些不需要的功能,低层次的概念可以更加高效。遵循这一原则的例子是,我们选择 LOG 操作码作为向 dapp 提供信息的方式,而不是像之前那样记录下所有交易和消息。在早先,“消息(message)” 的概念完完全全是多种概念的集合,它包含 “函数调用(function call)” 和 “外在观察者感兴趣的事件信息(event)” ,而两者是完全可以分离开来的。
没有特点就是最大的特点:为了遵循泛化原则,我们拒绝将那些高级用例内嵌为协议的一部分,哪怕是经常使用的用例,也绝不这么做。如果人们真的想实现这些用例,可以在合约内创建子协议(如,基于以太坊的子货币,比特币/莱特币/狗币的侧链等)。比如,在以太坊中就缺少类似比特币中的 “时间锁” 功能。但是,通过以下协议可以模拟出这个功能:用户发送签名数据包到特定的合约中处理,如果数据包在特定合约中有效,则执行相应的函数。
不厌恶风险:如果风险的增加带来了可观的好处,我们愿意承担更高的风险(例如,通用的状态转换,出块时间减低 50 倍,共识效率,等等)。
这些原则指导着以太坊的开发,但它们并不是绝对的;某些情况下,为了减少开发时间或者不希望一次作出过多改变,也会使我们推迟作出某些修改,把它留到将来的版本中去修改。
区块链层协议
本节对以太坊中区块链层协议的改变进行了描述,包括区块和交易是如何工作的、数据如何序列化及存储、账户背后的机制。
账户 ,而非 UTXO 1
比特币及其许多变种,都将用户的余额信息存储在 UTXO 结构中,系统的整个状态由一系列的 “未花费的输出” 组成(可以将这些 “未花费的输出” 想象成钱币)(校对注:更好的一个比喻可能是 “支票”。)。每个 UTXO 都有拥有者和自身的价值属性。一笔交易在消费若干个 UTXO 同时也会生成若干个新的 UTXO;而交易受到下列有效性要求的约束:
1.每个被引用的输入必须有效,且未被使用过;2.交易的签名必须与每笔输入的所有者签名匹配;3.输入的总值必须等于或大于输出的总值。
因此,比特币系统中,用户的 “余额” 是该用户的私钥能够有效签名的所有 UTXO 的总和。下图展示了比特币系统中交易输入输出过程:
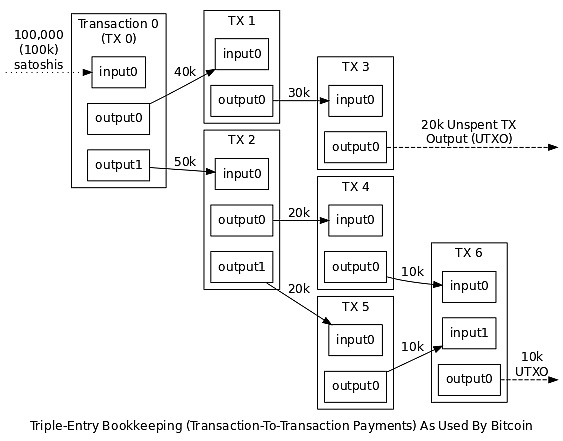
比特币所用的三式记账法
但是,以太坊抛弃了 UTXO 的方案,转而使用更简单的方法:采用状态(state)的概念存储一系列账户,每个账户都有自己的余额,以及以太坊特有的数据(代码和内部存储器)。如果交易发起方的账户余额足够支付交易费用,则交易有效,那么发起方账户会扣除相应金额,而接收账户则计入该金额。某些情况下,接收账户内有需要执行的代码,则交易会触发该代码的执行,那么账户的内部存储器可能会发生变化,甚至可能会创建额外的消息发送给其他账户,从而导致新的交易发生。
尽管以太坊没有采用 UTXO 的概念,但 UTXO 也不乏有一些优点:
较高程度的隐私保护:如果用户每次交易都使用一个新的地址,那么账户之间的相互关联就很困难。这样做适用于对安全性要求高的货币系统,但不是对任何 dapp 都合适。因为 dapp 通常需要跟踪用户复杂的绑定状态,而 dapp 的状态并不能像货币系统中的状态那样简单地划分。
潜在的可扩展性:理论上来说,UTXO 与某些类型的可扩展性方案(scalability paradigm)更契合,因为只需持币者拥有能够证明自己货币所有权的默克尔证明即可,即使所有的人(包括 TA 本人)都遗忘了这一数据,真正受损也这个人,其他人不受影响。在以太坊账户系统中,如果所有人都丢失了某个账户对应的默克尔树部分,那么该账户将无法处理任何能够影响它的消息,包括发送给它的消息,它也无法处理。不过,并非只有 UTXO 能够可扩展,也存在不依赖 UTXO 就能扩展的方式(此处没有扩展开来讲,译者注)。
账户的好处有以下几点:
节省大量空间:如果一个账户有 5 个 UTXO,则从 UTXO 模式转成账户模式,所需空间会从 300 字节降到 30 字节。具体计算如下:300 = (20+32+8)* 5 (20 是地址字节数,32 是 TX 的 id 字节数,8 是面额占用的字节数); 30 = 20 + 8 + 2 (20 是地址字节数,8 是账户余额值字节数,2 是 nonce 2 字节数);但实际节约并没有这么大,因为账户需要被存储在帕特里夏树中。另外以太坊中交易也比比特币中的更小(以太坊中 100 字节,比特币中 200-250 字节),因为每次交易只需要生成一次引用,一次签名,以及一个输出。
可互换性更强:UTXO 结构并没有区块链层的概念,所以不管是在技术还是法律上,通过建立一个红名单/黑名单,并依据的这些 “有效输出” 的来源区分它们并不是很实际。
简单:以太坊编码更简单、更易于理解,尤其是在涉及到复杂脚本时。尽管任何去中心化应用都可以用 UTXO 方式来(勉强)实现,但这种方式实质上是赋予脚本限制给定的 UTXO 所能输出的 UTXO 的种类及其使用条件(比如需要包含默克尔树证明来帮助脚本所对应的应用更改状态根)的能力。因此,UTXO 实现方式比以太坊使用账户的方式要复杂的多。
轻客户端:轻客户端可以随时通过沿指定方向扫描状态树来访问与账户相关的所有数据。在 UTXO 范式中,每笔交易需要用到的引用都不同,这对于长时间运行并使用了上文提到的 UTXO 根状态传播机制的 dapp 应用来说,无疑是繁重的。
我们认为,账户的好处大大超过了其他方式,尤其是对于我们想要支持的、可包含任意状态和代码的 dapp 应用而言。另外,本着 “没有特点就是最大的特点” 的指导原则,我们认为如果用户真的关心私密性,则可以通过合约中的签名数据包协议来建立一个加密 “混币器(mixer and coinjoin)” 混淆支付路径。
账户方式的一个弱点是:为了阻止重放攻击(replay attack,指让同一笔交易重复执行),每笔交易必须有一个 “nonce”(流水号)。因此,每个账户都要有一个实时更新的 nonce 值,每一笔新交易都在账户 nonce 值上递增 1 作为自己的 nonce(并在交易处理之后按此值更新账户的 nonce 值)(校对注:在账户模式下,如果交易不附带这种消耗性的标识符,交易就可被重复处理,这样接收账户可以一遍又一遍地收账且不用付出任何代价,而发账的账户会被吸干;以太坊账户的 nonce 随所发起的交易得到处理而递增,就解决了这个问题)。这就意味着,即使不再使用的账户,也不能从账户状态中移除。解决这个问题的一个简单方法是让交易包含一个区块号,使它们在一段时间后就无法再被重放,并且每隔一段时间段重置 nonce。
若要在状态中删除某个账户(比如长期不使用的账户),就必须先 “ping” 出它们来,而完整扫描区块链协议的开销是非常大的。在1.0上我们没有实现这个机制,1.1及以上版本可能会使用这个机制。
校对注:这就是以太坊日后面临的 “状态爆炸” 问题的技术原因:所有状态数据必须完整保存,无法合理地删除账户。作为一种区块链协议,以太坊的节点不仅要对事务(交易)的顺序达成共识,还要对全局状态达成共识(表现形式就是区块头里需要包括状态根。因此,若要删除状态,也需要全网的共识,否则会陷入分裂。
校对注:这种以 nonce 来标记账户交易顺序的做法,也使得用户的交易必须顺序执行,如果一笔交易无法得到处理,使用后续 nonce 的交易也无法得到处理。关于 “加速” 已发出的交易的上链进度,见这篇文章。
默克尔帕特里夏树(MPT)
默克尔帕特里夏树(Merkle Patricia tree/trie),由 Alan Reiner 提出设想,并在瑞波协议中得到实现,是以太坊的主要数据结构,用于存储所有账户状态,以及每个区块中的交易和收据数据。MPT 是默克尔树和帕特里夏树的结合,结合这两种树创建的结构具有以下属性:
任一组 键-值对 所对应的根哈希值都是唯一的,想要谎称某个 键值对 存在于某棵树上是一定会被识破的(除非攻击者拥有约 2^128 的算力)。
增、删、改 一个键值对的时间复杂度是对数级别。
MPT为我们提供了一个高效、易更新、且代表整个状态树的 “指纹” 。关于MPT更详细描述:https://github.com/ethereum/wiki/wiki/Patricia-Tree。
MPT的具体设计决策如下:
有两类节点:KV 节点和离散节点。KV节点的存在提高了效率,因为如果在特定区域树是稀疏的,KV节点可作为一个 “捷径” 来压缩树的高度(阅读 MPT 的详述可了解更多细节)。
离散节点是十六进制,不是二进制:这样让查找更有效率,我们现在认识到这种选择并不理想,因为十六进制树的查找效率在二进制中可以通过批次存储节点来模拟。但是,MPT 树结构的实现是非常容易出错的,最终至少会造成状态根不匹配,所以我们决定搁置变更,等到 1.1 版本再说。
空值(empty value)与非成员(non-membership)之间没有区别:这样做是为了简化逻辑,以太坊中未启用的账户的值(余额)默认为 0,空字符串也用 0 表示。然而,需要强调的是,这样做牺牲了一些通用性,因而也不是最优的。
终节点(terminating)和非终节点的区别:技术上,标识一个节点 “是否是终节点” 是没必要的,因为以太坊中所有的树都被用于存储固定长度(即键的长度)的数据,但为了增加通用性,我们还是会添加这个标识,以期望以太坊的 MPT 的实现方式能够被其他密码学货币原样采纳。
在 “安全树”(状态树和账户存储树)中采用 SHA3(k) 作为键:使用 SHA3(k),想要通过生成许多的账户(账户最多可让状态树高达 64 层!)并重复调用 SLOAD 和 SSTORE 操作码来 DoS 攻击的难度会大大提高。注意,这也让枚举树变得更困难;如果要使你的客户端具备枚举的功能,最简单的方法就是维护一个映射
sha3(k) -> k的数据库。
校对注:这里的意思是,如果使用 k 作为默克尔树存储数据的键,其分布可能很稀疏,而攻击者可以容易地规划出需要很深的树路径来存储的账户,并对这些账户重复调用状态访问操作,以此造成网络中的节点超负荷运行,但是,哈希函数的结果是随机分布的,以 sha3(k) 作为键可以使键的分布较为均匀,树高也会较矮)。
这种特性也是有得有失,这一方面意味着 DoS 攻击会变得更困难,另一方面,也使得一个区块中的交易的状态树访问路径,很少有重合的,因此每次搜索都是复杂度最差的情形。
此外,这也使得 MPT 不宜实现 “无状态性”(区块自身携带验证所需的数据、验证者无需具有全局状态),因为状态访问的路径不重合,证据的空间效率也是最差情形。当然,也可以说,默克尔树证据的空间效率本身也不够高
RLP
RLP(recursive length prefix):递归长度前缀。
RLP 编码是以太坊中主要的序列化格式,它的使用无处不在:区块、交易、账户状态以及网络协议消息。详见 RLP 正式描述: https://github.com/ethereum/wiki/wiki/RLP
RLP 旨在成为高度简化的序列化格式,它唯一的目的是存储嵌套的字节数组 3。不同于 protobuf、BSON 等现有的解决方案,RLP并不定义任何指定的数据类型,如 Boolean(布尔值)、float(浮点数)、double 或者 integer(整数)。它仅仅是以嵌套数组的形式存储结构体,由协议来确定数组的含义。RLP 也没有显式支持 map 集合,半官方的建议是采用 [[k1, v1], [k2, v2], ...] 的嵌套数组来表示键值对集合,k1,k2 ... 按照字符串的标准排序。
与 RLP 具有相同功能的方案是 protobuf 或 BSON,它们是一直被使用的算法。然而,以太坊中,我们更偏向于使用 RLP,因为:(1)它易于实现;(2)绝对保证字节的一致性。
许多语言的键值对集合没有明确的排序,并且浮点格式有很多特殊情况,这可能造成相同数据却产生不同编码和不同哈希值。通过内部开发协议,我们能确保它是带着这些目标设计的(这是一般原则,也适用于代码的其他部分,如虚拟机)。BitTorrent 使用的编码方式 bencode 也许可以替代 RLP。不过它采用的是十进制的编码方式,与采用二进制的 RLP 相比,稍微逊色了点。
压缩算法
网络协议和数据库都采用了一个自定义的压缩算法来存储数据。该算法可描述为:对 0 使用行程编码 4 并同时保留其他值(除了一些特殊情况如 sha3(' ') ),举例如下:
>>> compress('horse')'horse'>>> compress('donkey dragon 1231231243')'donkey dragon 1231231243'>>> compress('xf8xafxf8xabxa0x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00xbe{bxd5xcdx8dx87x97')'xf8xafxf8xabxa0xfex9exbe{bxd5xcdx8dx87x97'>>> compress("xc5xd2Fx01x86xf7#压缩算法存在之前,以太坊协议的许多地方都有一些特殊情况,例如,sha3 经常被重定义使得 sha3(' ')=' ',这样不需要在账户中存储代码,可以节省 64 字节。然而,最近所有这些使得以太坊数据结构变得臃肿的特殊情况都被删除了,取而代之的是将数据保存函数添加到区块链协议之外的层,也就是将其放入网络协议以及将其插入用户数据库实现。这样增加了模块化能力,简化了共识层,使得对压缩算法的持续更新部署起来相对简单(例如:可通过网络协议的版本号来区别、部署)。
树(trie)的使用
提醒:理解这部分的知识需要读者了解布隆过滤器 5 的原理。简介可见:http://en.wikipedia.org/wiki/Bloom_filter
以太坊区块链中每个区块头都包含指向三个树的指针:状态树、交易树、收据树。
状态树代表处理完该区块后的整个状态;
交易树代表区块中所有交易,这些交易由 index 索引作为key;(例如,k0:第一个执行的交易,k1:第二个执行的交易)
收据树代表每笔交易相应的收据。
交易的收据是一个 RLP 编码的数据结构:
[ medstate, gas_used, logbloom, logs ]其中:
medstate:交易处理后,状态树的根;
gas_used:交易处理后,gas 的使用量;
logs:是许多 [address, [topic1, topic2...], data] 元素的列表。这些元素由交易执行期间调用的操作码 LOG0 ... LOG4 生成(包含主调用和子调用);address 是生成日志的合约的地址;topics 是最多 4 个 32 字节的值;data 是任意大小的字节数组;
logbloom:交易中所有 logs 的 address 和 topics 组成的布隆过滤器。
区块头中也存在一个布隆过滤器,它是区块中交易的所有布隆过滤器的或运算(OR)结果。这样的构造使得以太坊协议对轻客户端友好得无以复加。
注释:
UTXO:unspent transaction outputs,字面理解是:未花费的交易输出,也即未被任何交易引用为输入的交易输出。它是比特币协议中用于存储价值(所有权)信息的数据结构。—— 校对注
Nonce,Number used once 或 Number once 的缩写,在密码学中 Nonce 是一个只被使用一次的任意或非重复的随机数值,在加密技术中的初始向量和加密哈希函数都发挥着重要作用,在各类验证协议的通信应用中确保验证信息不被重复使用以对抗重放攻击(Replay Attack)。—— 译者注
嵌套数组:创建一个数组,并使用其他数组填充该数组。如数组 pets:
var cats : String[] = ["Cat","Beansprout", "Pumpkin", "Max"];
var dogs : String[] = ["Dog","Oly","Sib"];
var pets : String = [cats, dogs];
—— 译者注
行程编码(run-length-encoding):一种统计编码。主要技术是检测重复的比特或字符序列,并用它们的出现次数取而代之。(百度百科)—— 译者注
布隆过滤器:由 Howard Bloom 在 1970 年提出的二进制向量数据结构,它具有很好的空间和时间效率,被用来检测一个元素是不是集合中的一个成员。(百度百科)—— 译者注




